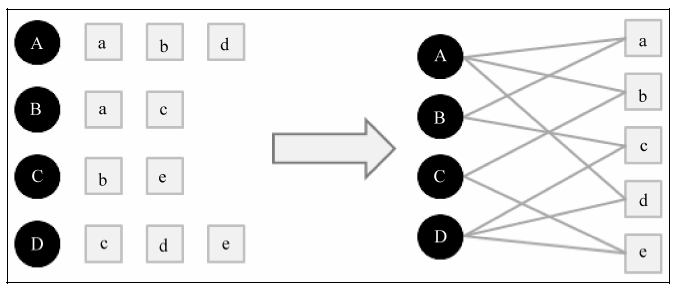
It is about Recommendation System.
2.5 隐语义模型
2.5.1 基础算法
LFM(latent factor model)隐语义模型最早在文本挖掘领域被提出,用于找到文本的隐含语义,它的核心思想就是通过隐含特征联系用户兴趣和物品。其基本方法就是,当我们需要对某用户进行推荐的时候,我们可以首先对物品的兴趣进行分类。对于某用户,我们可以首先得到他的兴趣分类,然后从分类中挑选他可能喜欢的物品。
因而,我们可以总结出,基于兴趣分类的方法大体上需要解决三个问题:
- 如何给物品进行分类?
- 如何确定用户对哪些类的物品感兴趣,以及感兴趣的程度?
- 对于一个给定的类,选择哪些属于这个类的物品推荐给用户,以及如何确定这些物品在 一个类中的权重?
传统的方式就是通过编辑进行分类,但是即使使用很系统的分类体系,编辑给出的分类仍然具有不少的缺点,如分类的粒度、多维度分类、分类权重等等。因而,科研人员提出从数据本身出发自动寻找这些类,即隐含语义分析技术(latent variable analysis)。其采用采取基于用户行为统计的自动聚类,能够很好地解决传统编辑出现的问题。
隐含语义分析技术已经产生了很多模型与方法,以LFM为例,其通过如下公式计算用户u对物品i的兴趣:
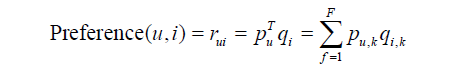
这个公式中Pu,k和qi,k是模型的参数,其中Pu,k度量了用户u的兴趣和第k个隐类的关系,而qi,k度量了第k个隐类和物品i之间的关系。那么最关键的问题就是对着两个的参数的计算。要先计算着两个参数,需要使用一个训练集,通过学习该数据集来获得模型参数。不过在此处,我们讨论的是隐性反馈数据集,这种数据集的特点是只有正样本(用户喜欢什么物品),而没有负样本(用户对什么物品不感兴趣)。
那么我们发现LFM推荐系统的第一个关键问题就是为用户生成负样本。在进行镦粗测算之后发现,负样本应该满足如下的原则:
- 对每个用户,要保证正负样本的平衡;
- 对每个用户采集负样本时,要选取那些很热门,而用户没有行为的物品。
因而我们可以得出采集负样本的代码如下:
def RandomSelectNegativeSample(self, items):
ret = dict()
for i in items.keys():
ret[i] = 1
n = 0
for i in range(0, len(items) * 3):
item = items_pool[random.randint(0, len(items_pool) - 1)]
if item in ret:
continue
ret[item] = 0
n + = 1
if n > len(items):
break
return ret
items_pool维护了候选物品的列表,在这个列表中,物品i出现的次数和物品i的流行度成正比。items是一个dict,它维护了用户已经有过行为的物品的集合。代码中将范围上限设为len(items) * 3,主要是为保证正、负样本数量接近。经过采样,我们就可以得到综合的用户-物品集k={(u,i)},其中如果(u, i)是正样本,则有 rui=1,否则有rui=0。然后,需要优化如下的损失函数来找到最合适的参数p和q:
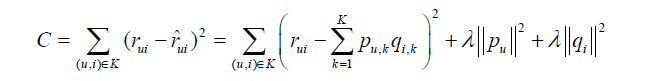
公式中的最后两项是用来防止过拟化的正则化项,λ可以通过实验获得。要最小化上面 的损失函数,可以利用一种称为随机梯度下降法的算法。损失函数主要有两个参数puk和qik。首先要对他们求偏函数,得到:
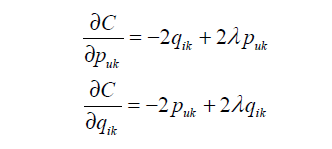
根据随机梯度下降法,我们需要将参数沿着最快下降方向向前推进,由此得到如下递推公式:
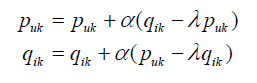
其中α是学习速率,可以通过不断实验获得。
如上的优化过程的代码如下:
def LatentFactorModel(user_items, F, N,alpha, lambda):
[P, Q] = InitModel(user_items, F)
for step in range(0,N):
for user, items in user_items.items():
samples = RandSelectNegativeSamples(items)
for item, rui in samples.items():
eui = rui - Predict(user, item)
for f in range(0, F):
P[user][f] += alpha * (eui * Q[item][f] - lambda * P[user][f])
Q[item][f] += alpha * (eui * P[user][f] - lambda * Q[item][f])
alpha *= 0.9
def Recommend(user, P, Q):
rank = dict()
for f, puf in P[user].items():
for i, qfi in Q[f].items():
if i not in rank:
rank[i] += puf * qfi
return rank
在计算LFM的性能时,我们也使用离线实验进行评测。在LFM中,有四个重要的参数需要被考虑:
- 隐特征的个数F
- 学习效率alpha
- 正则化参数lambda
- 负样本/正样本比例 ratio
在实际的实验中我们发现,ratio对LFM的性能影响是最大的。在一定程度上,ratio参数控制了推荐算法发掘长尾的能力。当数据集非常稀疏时,LFM的性能会非常明显地下降。
2.5.2 LFM和基于领域的方法的比较
LFM是一种基于机器学习的推荐系统,它是一种学习方法,通过优化一个设定的指标建立最优的模型。当用户量非常大的时候,LFM就会体现出它的优势,由于它大量节省了训练过程中的内存,因此收到青睐。但LFM并不太适合于物品数非常庞大的系统。而且LFM并不能在线计算,需要将计算结果存储在数据库中,因而LFM并不能进行在线实时推荐。
2.6 基于图的模型
2.6.1 基础算法
因为在实验中我们可以使用二元组(u, i)表示用户u对物品i产生过行为,这种数据集我们就能用一个二分图。如下图: