It is about Recommendation System.

推荐系统

一、基础知识

1.1 推荐系统简介

推荐系统就是自动联系用户和物品的一种工具，它能够在信息过载的环境中帮助用户发现令他们感兴趣的信息，也能将信息推送给对它们感兴趣的用户。和搜索引擎一样，推荐系统也是一种帮助用户快速发现有用信息的工具。和搜索引擎不同的是，推荐系统不需要用户提供明确的需求，而是通过分析用户的历史行为给用户的兴趣建模，从而主动给用户推荐能够满足他们兴趣和需求的信息。

常见的集中推荐的方式：

• 社会化推荐（social recommendation）

• 基于内容的推荐 （content-based filtering）

• 基于协同过滤的推荐（collaborative filtering）

1.2 个性化推荐系统的应用

• 电子商务（例如亚马逊这种）

• 电影和视频网站

• 个性化音乐网络平台

• 社交网络

• 个性化广告（上下文广告、搜索广告、个性化展示广告）

• ….

1.3 推荐系统评测

1.3.1 评测推荐效果的实验方法

• 离线实验

• 用户调查

• 在线实验

1.3.2 评测指标

• 用户满意度

  主要通过调查问卷的形式来获得；

• 预测准确度

  • 该指标主要通过离线实验的方式计算，需要一个数据集，分成训练集和测试集，通过计算预测行为和测试集上实际行为的重合度作为预测准确度。

  • 分为不同的预测方向，如评分预测（通过均方根误差（RMSE）和平均绝对误差（MAE）计算）、TopN推荐（通过准确率（precision）/召回率（recall）度量）等。

• 覆盖率

  • 简而言之就是推荐系统能够推荐出来的物品占总物品集合的比例，这个指标主要被提供商所关心。

  • 主要的计算公式如下：

  

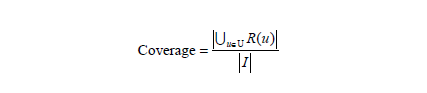
  • 可以使用信息熵和基尼系数来计算覆盖率。

• 多样性

  • 如果推荐列表比较多样，覆盖了用户绝大多数的兴趣点，那么就会增加用户找到感兴趣物品的概率。因此给用户的推荐列表也需要满足用户广泛的兴趣，即具有多样性。

  • 用户推荐列表多样性的计算：

  

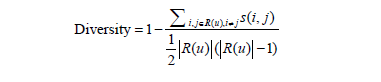
  • 系统推荐多样性的计算：

  

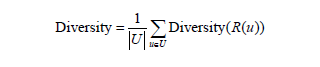
• 新颖度

• 惊喜度

• 信任度

• 实时性

• 健壮性

二、利用用户行为数据

2.1 用户行为数据简介

用户行为数据在网站上最简单的存在形式是日志。一般用户行为在个性化推荐系统中分为两种：显性反馈行为、隐性反馈行为。显性反馈行为指用户明确表示对物品喜好的行为，而隐性反馈行为指的是那些不能明确反应用户喜好的行为。

一般情况下用户的行为大体上可以被如下几个参数包括：

user id：产生行为的用户的唯一标识

item id：产生行为的对象的唯一标识

behavior type：行为的种类（比如是购买还是浏览）

context：产生行为的上下文，包括时间和地点等

behavior weight：行为的权重

behavior content：行为的内容

2.2 用户行为分析

2.2.1 用户活跃度和物品流行度的分布

一句话就是，用户活跃度和物品流行度基本上符合长尾分布。

2.2.2 用户活跃度和物品流行度的关系

主要研究不同活跃度的用户喜欢的物品的流行度是否有差别。研究的结果是，一般来说，用户越活跃，越倾向于浏览冷门的物品。基于用户行为数据设计的推荐算法一般称为协同过滤算法。其中最广泛应用的是基于领域的方法，主要包括两种算法：基于用户的协同过滤算法和基于物品的协同过滤算法。

2.3 实验设计和算法评测

2.3.1 实验设计

将用户行为数据集按照均匀分布随机分成M份，挑选一份作为测试集，将剩下的M-1份作为训练集。然后在训练集上建立用户兴趣模型，并在测试集上对用户行为进行预测，统计出相应的评测指标。

产生训练集和测试集的方法是：

def SplitData(data, M, k, seed):
	test = []
	train = []
	random.seed(seed)
	for user, item in data:
	if random.randint(0,M) == k:
		test.append([user,item])
	else:
		train.append([user,item])
	return train, test

2.3.2 评测指标

在评测指标中，对用户u推荐N个物品（记为R(u)），令用户u在测试集上喜欢的物品集合为T(u)，所有物品的集合为I。

• 召回率

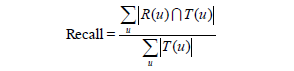
• 准确率

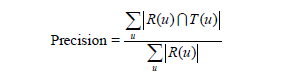
• 覆盖率

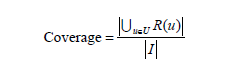
• 新颖度

2.4 基于领域的算法

2.4.1 基于用户的协同过滤算法

• 基础算法

简而言之就是，在一个在线个性化推荐系统中，当一个用户A需要个性化推荐时，可以先找到和他有相似兴趣的其他用户，然后把那些用户喜欢的、而用户A没有听说过的物品推荐给A。这种方法称为基于用户的协同过滤算法。

因而在这个算法中主要包括两个步骤，一是找到与目标用户兴趣相似的用户合集，二是合集中用户喜欢的，但是目标用户没有听过的物品。

首先计算两个用户的相似程度。给定用户u和用户v，令N(u)表示用户u曾经有过正反馈的物品集合，令N(v)为用户v曾经有过正反馈的物品集合。那么，我们可以通过如下的Jaccard公式简单地计算u和v的兴趣相似度：

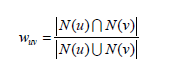
或者我们可以使用余弦相似度来进行计算：

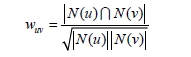
但是这里涉及到一个问题就是，如果我们对集合中的所有两两用户都进行余弦相似度的计算，那么计算的时间复杂度就太大了，为O(|U|*|U|)。实际上绝大多数用户相互之间没有对相同的物品产生过行为。可以首先建立物品到用户的倒排表，对于每个物品都保存对该物品产生过行为的用户 列表。令稀疏矩阵C[u][v]= N(u) N(v) 。那么，假设用户u和用户v同时属于倒排表中K个物品对 应的用户列表，就有C[u][v]=K。从而，可以扫描倒排表中每个物品对应的用户列表，将用户列 表中的两两用户对应的C[u][v]加1，最终就可以得到所有用户之间不为0的C[u][v]。最后用这个矩阵除以对应分母部分，即可得到最终的相似度矩阵。

python的实现代码如下：

def UserSimilarity(train):
	# build inverse table for item_users
	item_users = dict()
		for u, items in train.items():
			for i in items.keys():
				if i not in item_users:
					item_users[i] = set()
				item_users[i].add(u)

	#calculate co-rated items between users
	C = dict()
	N = dict()
	for i, users in item_users.items():
		for u in users:
			N[u] += 1
			for v in users:
				if u == v:
					continue
				C[u][v] += 1

	#calculate finial similarity matrix W
	W = dict()
	for u, related_users in C.items():
		for v, cuv in related_users.items():
			W[u][v] = cuv / math.sqrt(N[u] * N[v])

	return W

得到用户相似度之后，UserCF算法会给用户推荐和他兴趣最相似的k个用户喜欢的物品。我们使用如下公式度量UserCF算法中用户u对物品i的感兴趣程度：

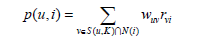
因为使用的是单一行为的隐反馈数据，所以所有的rvi=1。

实现算法如下：

def Recommend(user, train, W):
	rank = dict()
	interacted_items = train[user]
	for v, wuv in sorted(W[u].items, key=itemgetter(1), reverse=Tr[0:K]:
		for i, rvi in train[v].items:
			if i in interacted_items:
				#we should filter items user interacted before
				continue
			rank[i] += wuv * rvi
	return rank

在实现了最终的推荐结果后，我们就要考虑该系统的推荐效率了。。UserCF只有一个重要的参 数K，即为每个用户选出K个和他兴趣最相似的用户，然后推荐那K个用户感兴趣的物品。我们对值的调整会对推荐算法的各种指标产生一定的影响。因此，离线实验需要测量不同K值下UserCF算法的性能指标，最终获得最佳的K值。

• 用户相似度计算的改进

在实际的推荐系统中，某物品尽管被两个用户购买，但是这并不能反映这两个用户的兴趣相同，只是因为该物品时人人会购买的热门物品。因此在可以改进算法，惩罚用户u和用户v共同兴趣列表中热门物品对他们相似度的影响。因而改进型的兴趣相似程度的计算方法是：

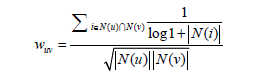
注：是log(1+|N(i)|)

改进后的算法叫做User-IIF算法，改进型计算相似度的方法如下：

def UserSimilarity(train):
	# build inverse table for item_users
	item_users = dict()
	for u, items in train.items():
		for i in items.keys():
			if i not in item_users:
				item_users[i] = set()
			item_users[i].add(u)
	#calculate co-rated items between users
	C = dict()
	N = dict()
	for i, users in item_users.items():
		for u in users:
			N[u] += 1
			for v in users:
				if u == v:
					continue
				C[u][v] += 1 / math.log(1 + len(users))
	#calculate finial similarity matrix W
	W = dict()
	for u, related_users in C.items():
		for v, cuv in related_users.items():
			W[u][v] = cuv / math.sqrt(N[u] * N[v])
	return W

2.4.2 基于物品的协同过滤算法

• 基础算法

基于物品的协同过滤算法是目前业界使用最多的算法。基于物品的协同过滤算法（简称ItemCF）给用户推荐那些和他们之前喜欢的物品相似的物品。比如，该算法会因为你购买过《数据挖掘导论》而给你推荐《机器学习》。不过，ItemCF算法并不利用物品的内容属性计算物品之间的相似度，它主要通过分析用户的行为记录计算物品之间的相似度。该算法认为，物品A和物品B具有很大的相似度是因为喜欢物品A的用户大都也喜欢物品B。

基于物品的协同过滤算法主要分为两步：

1. 计算物品之间的相似度；
2. 根据物品的相似度和用户的历史行为给用户生成推荐列表。

首先，我们可以使用如下公式进行物品i与j的相似度的计算：

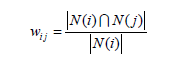
其中分母|N(i)|是喜欢物品i的用户数，而分子 N(i) N( j) 是同时喜欢物品i和物品j的用户 数。。如果物品j很热门，很多人都喜欢，那么Wij就会很大，接近1。因此，该公式会造成任何物品都会和热门的物品有很大的相似度，因而我们要使用改进公式来避免推荐出热门的物品。如下公式：

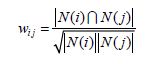
首先第一步，，用ItemCF算法计算物品相似度时也可以首先建立用户—物品倒排表（即对每个用户建立一个包含他喜欢的物品的列表），然后对于每个用户，将他物品列表中的物品两两在共现矩阵C中加1。代码如下：

def ItemSimilarity(train):
	#calculate co-rated users between items
	C = dict()
	N = dict()
	for u, items in train.items():
		for i in users:
			N[i] += 1
			for j in users:
				if i == j:
					continue
				C[i][j] += 1
	#calculate finial similarity matrix W
	W = dict()
	for i,related_items in C.items():
		for j, cij in related_items.items():
			W[u][v] = cij / math.sqrt(N[i] * N[j])
	return W

在实际的操作中，我们首先可以得到一个物品相互关系的矩阵，记录某对物品同时出现在n个用户的物品集合里，在得到这个矩阵之后，我们将矩阵归一化即可得到物品之间的余弦相似度矩阵w。这个方法好处就是，尽管在计算过程中没有利用任何内容属性，但利用ItemCF计算的结果却是可以从内容上看出某种相似度的。

在得到物品相似度之后，ItemCF可以使用公式来计算用户u对一个物品j的兴趣了：

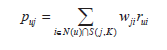
这里N(u)是用户喜欢的物品的集合，S(j,K)是和物品j最相似的K个物品的集合，wji是物品j和i 的相似度，rui是用户u对物品i的兴趣。实现代码如下：

def Recommendation(train, user_id, W, K):
	rank = dict()
	ru = train[user_id]
	for i,pi in ru.items():
	for j, wj in sorted(W[i].items(), key=itemgetter(1), reverse=True)[0:K]:
		if j in ru:
			continue
		rank[j] += pi * wj
	return rank

在进行算法设计之后，确定k的值是至关重要的，因为k值会影响数据集上ItemCF算法离线实验的各项性能指标的评测结果。因此通过评测在不同k值下精度、流行度、覆盖率等的变化，我们就能确定一个最佳的k值。

• 用户活跃度对物品相似度的影响

在此处，我们需要讨论的是热门用户对整个相似度矩阵的影响。因而，在改进型计算相似度的算法中引进了IUF的概念，形成新的相似度的计算公式如下：

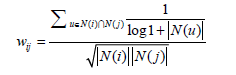
或者说，对于过分活跃的用户，我们采取直接忽略他的兴趣列表的方式，形成了ItemCF-IUF算法，这种算法明显提高了推荐结果的覆盖率，降低了推荐结果的流行度，提升了综合性能。

• 物品相似度的归一化

在实际的研究中，我们发现将ItemCF的相似矩阵归一化，能够提高推荐的准确率，公式如下：

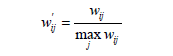
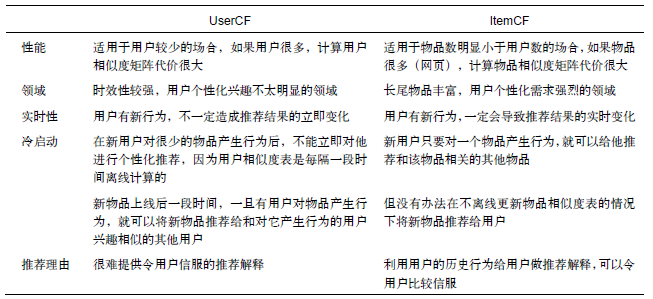
2.4.3 UserCF和ItemCF优缺点的对比

• Previous
  About MapReduce
• Next
  Recommendation System Chapter2